http://cpp.gantep.edu.tr
C++ resources. Faculty of Engineering, University of Gaziantep
 MAIN  -  Tutorials  -  Howtos  -  nmPrimer  -  Misc  -  Links  -  Contacts
Last modified: Sat, 31 Oct 2009 12:23:17 +0200

Complete: ##################-- (90%)

Differentiation of a function f(x)
1.   The Central Difference Approximation (CDA)
2.   The Richardson Extrapolation Method
The derivative f'(x) of a function f(x) is simply the gradient of the function at a point x. Finding the derivative of a function analytically may be difficult and so a numerical solution may be necessary or simply convenient. The following sections describe two methods of differentiation, both are based on the approximation of the gradient of f(x) around a value x.

1.   The Central Difference Approximation (CDA)

In the figure below, the gradient of the function at x is approximated by the line drawn from x-h to x+h. This is called the Central Difference Approximation (CDA). Intuitively this approximation looks right, and as h reduces in size the approximation should improve. Below the diagram is the proof from Taylor's expansion that the CDA does return the first derivative with an error of approximately h2/6 f'''(x); i.e. the error is proportional h2. The value of h should therefore be chosen to be small, however if it is too small then round-off errors will dominate the total error. The choice of h may therefore require some experimentation.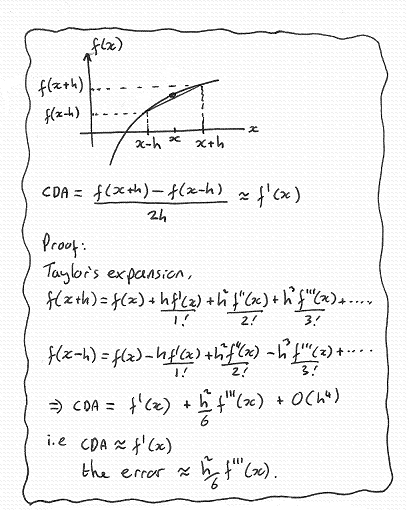

The CDA is implementated in the program below.

nmprimer-CDA.cpp: Central Difference Approximation (CDA) for the derivative of a function.
  1:
  2:
  3:
  4:
  5:
  6:
  7:
  8:
  9:
 10:
 11:
 12:
 13:
 14:
 15:
 16:
 17:

// Central Difference Approximation (CDA) for the derivative of a function f(x)
// For f(x) = x^4 the analytical solution is 4x^3 e.g. f'(3.5)=171.5
#include <iostream>
#include <iomanip>
using namespace std;

double f(double x) { return x*x*x*x; } // The function f(x)

int main() {

  double  x=3.5, h=0.001;
  double CDA = (f(x+h)-f(x-h))/(2*h);

  cout << setprecision(8) << fixed;
  cout << "CDA = " << CDA << endl;

}
 
CDA = 171.50001400

In this program the derivative of the function f(x) = x 4 is evaluated at x=3.5. The analytical solution f'(3.5)=4 * 3.53 = 171.5. The result from the CDA is 171.500014 and so the error is 171.500014 - 171.5 = 0.000014 is consistent with the expected error h2/6 f'''(x) = 0.0012/6 * 24 * 3.5 = 0.000014. This error is called a truncation error as it represents the truncation of higher-order terms in the exact expansion of the derivative. Reducing the size of h will reduce the truncation error. However, round-off errors will increase as h becomes very small. You can investigate round-off and truncation errors by playing with the value of h in the above program.

2.   The Richardson Extrapolation Method

The Richardson Extrapolation Approximation (REA) provides a higher-order approximation, i.e. the truncation error is proportional to a higher power of h and so is much smaller for h<<1. The truncation error in the REA is approximately h4/30 f`````(x). You can prove this by constructing the REA using Taylor's expansion as performed above for the CDA.

The REA is implementated in the program below.

nmprimer-REA.cpp: The Richardson Extrapolation Method for the derivative of a function.
  1:
  2:
  3:
  4:
  5:
  6:
  7:
  8:
  9:
 10:
 11:
 12:
 13:
 14:
 15:
 16:
 17:

// Richardson Extrapolation Aprroximation (REA) for the derivative of a function f(x)
// For f(x) = x^4 the analytical solution is 4x^3 e.g. f'(3.5)=171.5
#include <iostream>
#include <iomanip>
using namespace std;

double f(double x) { return x*x*x*x; } // The function f(x)

int main() {

  double  x=3.5, h=0.001;
  double REA = (f(x-2*h)-8*f(x-h)+8*f(x+h)-f(x+2*h))/(12*h);

  cout << setprecision(8) << fixed;
  cout << "REA = " << REA << endl;

}
 
REA = 171.50000000
Again, the derivative of the function f(x) = x 4 is evaluated at x=3.5. The solution 171.5 is consistent with the expected truncation error h4/30 f`````(x) = 0 as the fifth derivative of the function is zero.

Complete: ##################-- (90%)