http://cpp.gantep.edu.tr
C++ resources. Faculty of Engineering, University of Gaziantep
 MAIN  -  Tutorials  -  Howtos  -  nmPrimer  -  Misc  -  Links  -  Contacts
Last modified: Sat, 31 Oct 2009 10:13:41 +0200

Complete: ##################-- (90%)

Roots of a function f(x)
1.   The Newton Raphson Method
2.   The Secant Method
The root x0 of a function f(x) is such that f(x0)=0. Finding the root of a function analytically may be difficult and so a numerical solution may be necessary or simply convenient. The following sections describe two methods for find roots numerically, both are based on iterating improvements on an initial estimate of the root until the estimated error is less than a predetermined tolerance (required accuracy).

1.   The Newton Raphson Method

nmprimer-NewtonRaphson.cpp: Newton-Raphson method for finding roots of a function.
  1:
  2:
  3:
  4:
  5:
  6:
  7:
  8:
  9:
 10:
 11:
 12:
 13:
 14:
 15:
 16:
 17:
 18:
 19:
 20:
 21:
 22:
 23:
 24:
 25:
 26:
 27:

// Newton-Raphson method for the root of f(x)
// Analytically the solution is x^3-28 = 0
// => x = 28^(1/3) = 3.0365889718756625194208095785057...
#include <iostream>
#include <iomanip>
#include <cmath>
using namespace std;

double f(double x) { return x*x*x-28.; } // The function f(x)
double d(double x) { return 3*x*x; }     // The derivative of f(x)

int main() {

  double  x=3.5, Tolerance=1.0E-12;
  cout << setprecision(18) << fixed;

  do {

    double Error = f(x) / d(x);               // Estimate the error
    cout << "Root = " << x << " Error = " << Error << endl;

    if ( abs(Error) < Tolerance ) break;      // Terminate if the tolerance is satisfied
    x = x - Error;                            // Subtract the error estimate

  } while(1);

}
 
Root = 3.500000000000000000 Error = 0.404761904761904767
Root = 3.095238095238095344 Error = 0.057544848314079300
Root = 3.037693246924015877 Error = 0.001103873666278150
Root = 3.036589373257737812 Error = 0.000000401382022117
Root = 3.036588971875715526 Error = 0.000000000000053042

In this program an error estimate Error (calculated at line 19) is subtracted from the root estimate x (at line 23). This is iterated until the size of the error estimate is less than the tolerance (this termination condition is coded at line 22). The program requires an initial estimate of the root, and a tolerance (provided at line 14). Here the tolerance is 10-12 which means we require at least 12 decimal place accuracy (indicated by the underlined digits in the output field).

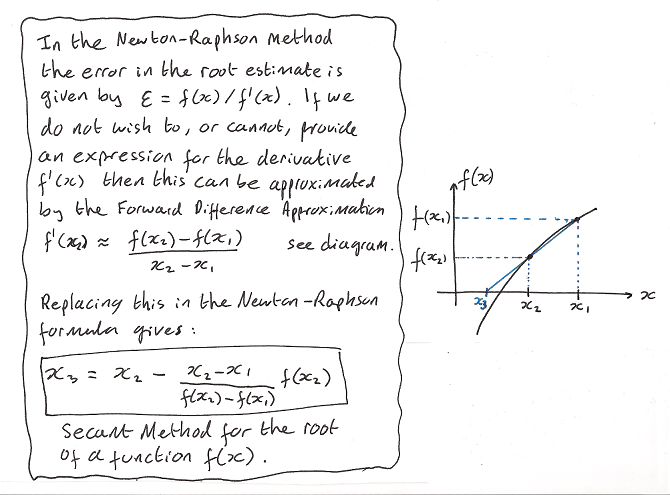
The error estimated calcuated as Error = f(x) / f'(x) provides very fast convergence with the number of correct significant figures typically doubling on each interation. The derivation of this method is given below:

2.   The Secant Method

nmprimer-SecantMethod.cpp: Secant Method for finding roots of a function.
  1:
  2:
  3:
  4:
  5:
  6:
  7:
  8:
  9:
 10:
 11:
 12:
 13:
 14:
 15:
 16:
 17:
 18:
 19:
 20:
 21:
 22:
 23:
 24:
 25:
 26:
 27:

// Secant Method for the root of f(x)
// Analytically the solution is x^3-28 = 0
// => x = 28^(1/3) = 3.0365889718756625194208095785057...
#include <iostream>
#include <iomanip>
#include <cmath>
using namespace std;

double f(double x) { return x*x*x-28.; } // The function f(x)

int main() {

  double  x2=3.5, x1=3.6, Tolerance=1.0E-12;
  cout << setprecision(18) << fixed;

  do {

    double Error = (x2-x1)/(f(x2)-f(x1))*f(x2); // Estimate the error
    cout << "Root = " << x2 << " Error = " << Error << endl;

    if ( abs(Error) < Tolerance ) break;        // Terminate if the tolerance is satisfied
    x1 = x2;                                    // Improve x1
    x2 = x2 - Error;                            // Improve x2

  } while(1);

}
 
Root = 3.500000000000000000 Error = 0.393414440624173245
Root = 3.106585559375826922 Error = 0.060452490895290242
Root = 3.046133068480536554 Error = 0.009327881945536839
Root = 3.036805186534999645 Error = 0.000215536543532409
Root = 3.036589649991467077 Error = 0.000000678067522840
Root = 3.036588971923944058 Error = 0.000000000048281500
Root = 3.036588971875662679 Error = 0.000000000000000128
This program has the same structure as the Newton-Raphson program except for three small modifcations. First we start with two initial estimates of the root (x1 and x2 at line 13). Second, the error estimate Error (calculated at line 18) does not require a knowledge of the derivative of the function. Third, both estimates x1 and x2 are improved first my replacing x1 with x2 (line 22) then by subtracting the error estimate from x1 (line 23). Again, the tolerance is 10-12 which means we require at least 12 decimal place accuracy (indicated by the underlined digits in the output field). Note that convergence is slightly slower in the Secant Method as the error estimate includes an estimate of the derivative of f(x).

The derivation of this method is given below:

Complete: ##################-- (90%)