http://cpp.gantep.edu.tr
C++ resources. Faculty of Engineering, University of Gaziantep
 MAIN  -  Tutorials  -  Howtos  -  nmPrimer  -  Misc  -  Links  -  Contacts
C++ Tutorial (Basic)
[index][<][1][2][3][4][5][6][7][8][9][>]

5. Functions I
Last modified: Thu, 03 Jun 2010 15:53:03 +0300

Complete: ###################- (95%)

5.1 Introduction
5.2 Function Concept
5.3 Using Functions
5.4 Function Prototypes
5.5 Return Values
5.6 void Functions
5.7 Many Functions
5.8 Examples
5.9 Exercises

5.1 Introduction

We have seen intrinsic functions such as the sin(), fabs() and sqrt() functions. In C++, additional functions can be defined by the programmer. These can be called programmer defined functions. Using functions one can structure a program in a more modular way, that is to say structured programming is supported by C++.

In this section we will look at how to write programmer defined functions.

5.2 Function Concept

A function is an object that accepts some inputs and then outputs a result depending on the inputs. Every function has a name and independent values of inputs. The inputs are called parameters or arguments.

Generally, a function can be represented by a box as shown in Fig 5.1.


Fig 5.1: Box notation of a function.

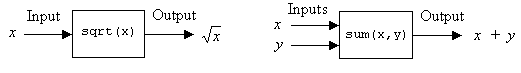
A function may have zero, one, or more inputs but it has only one output which is called the return value of that function. Fig 5.2 shows examples of one- and two-input functions:


Fig 5.2: Box notations of a one-input and two-input function.

In a programming language, a function is a group of statements that is executed when it is called from some point of the program. C++ allows users to write this type of function.

The general form of a function is: 

  type name(parameter1, parameter2, ...) { 
   ...
     statements
   ...
  }
where
  • type is the data type of the function (i.e. type of the return value) such as float.
  • name is a valid C++ identifier representing the name of the function.
  • parameters is a list of (input) arguments. Each consists of a data type followed by an identifier.
  • statements is the body of the function. These are executed when the function is called.
As an example, a function that returns the sum of two integers can be defined as follows: 
  int sum(int a, int b) {
    int c;
    c = a + b;
    return c;
  }
or 
  int sum(int a, int b) {
    int c = a + b;
    return c;
  }
or 
  int sum(int a, int b) {
    return a+b;
  }
where the return statement finalizes the function, and for this case, returns the sum of the arguments a and b back to the function where it is called.

5.3 Using Functions

Our first illustration is given in Program 5.1.

05prg01.cpp: Function example
  1:
  2:
  3:
  4:
  5:
  6:
  7:
  8:
  9:
 10:
 11:
 12:
 13:
 14:
 15:
 16:
 17:

// Function example
#include <iostream>
using namespace std;

int sum (int a, int b) {
  int c;
  c = a + b;
  return c;
}

int main ()
{
  int s;
  s = sum(22, 33);
  cout << "The sum is " << s << endl;
  return 0;
}
 
The sum is 55

As we previously stated, a C++ program always starts its execution by the main() function. The program begins by declaring a variable s of int type at line 13. Next, our function (sum()) is called at line 14 where two integer values are passed to the function: 22 and 33. These are called actual values and correspond to local variables int a and int b respectively. After passing values the program jumps to the 5th line to execute statements (body) of the function sum() which returns the value of the local variable c, containing a + b, back to the line 14 to assign the result (55) to the variable s. Finally, the program outputs the content of s at line 15 and finishes at line 16 by executing the return 0; statement. Note that the function sum() is defined before it is used, if the function is defined after it is used then a prototype should be declared (see Section 5.4 below).

For the sum() function, the matching between actual and local values can be represented as shown in Fig 5.3.


Fig 5.3: Matching between actual and local values in the function sum().

Any valid C++ expression can be a function argument, including constants, mathematical and logical expressions, and other functions that return a value. For example, the following calls of sum() are valid: 

    int x = 33, y = 66, i;
    float r;
    ...
    i = sum(x, y);
    i = sum(x, 3);
    r = sum(x, 5)/2.0;
    i = sum(x, sum(4,y) );
    i = sum(x, (x<y ? x : y) );

5.4 Function Prototypes

A function body can also be written after main() function. In this case, a function prototype has to be given before main(). The function prototype is a statement, which means it ends with a semicolon. It consists of the function's return type, name, and parameter list. According to this, the prototype of the sum() function is: 

    int sum (int a, int b);
However, the function prototype does not need to contain the names of the parameters. Just their types can be written as follows: 
    int sum (int, int);
Using prototype of sum(), Program 5.1 is rewritten as Program 5.2 below:

05prg02.cpp: Function example with prototype
  1:
  2:
  3:
  4:
  5:
  6:
  7:
  8:
  9:
 10:
 11:
 12:
 13:
 14:
 15:
 16:
 17:
 18:
 19:
 20:
 21:

// Function example with prototype
#include <iostream>
using namespace std;

// The function prototype of the sum
int sum(int, int);

int main ()
{
  int s;
  s = sum(22, 33);
  cout << "The sum is " << s << endl;
  return 0;
}

// The function definition of sum
int sum (int a, int b) {
  int c;
  c = a + b;
  return c;
}
 
The sum is 55

Program 5.3 contains another example function, it returns the surface area of a closed cylinder whose height is h and radius is r.

05prg03.cpp: Computing surface area of a closed cylinder
  1:
  2:
  3:
  4:
  5:
  6:
  7:
  8:
  9:
 10:
 11:
 12:
 13:
 14:
 15:
 16:
 17:
 18:
 19:
 20:
 21:
 22:
 23:
 24:
 25:

// Computing surface area of a cylinder
#include <iostream>
using namespace std;

// The prototype of cylinderArea
double cylinderArea(double, double);

int main ()
{
  double r, h, A;

  cout << "Input radius and height: ";
  cin >> r >> h;

  A = cylinderArea(r, h);

  cout << "The area is " << A << endl;

  return 0;
}

// Function definition of cylinderArea
double cylinderArea(double radius, double height) {
  return 2.0*3.14159265358979323846*radius*(radius + height);
}
 
Input radius and height: 2 1.5
The area is 43.9823

5.5 Return Values

The keyword return in a function has two jobs:

  • to form the return value of the function
  • to finalize the function
After the return statement, a variable, a constant, an expression or a function can be placed. For instance, 
     return (a+b/c);          // an expresion (use of paranthesis is optional)
     return 10;               // a constant
     return 1.0/sqrt(2.0*x);  // a function (first sqrt() is called)
A function may contain more than one return statement. However, the function is finalized after the first encounter of a return statement. For example, the following function has five return statements but only one value is returned. 
 char grade(float average)
 {
   if( average >= 0.  && average < 50. ) return 'F';
   if( average >= 50. && average < 70. ) return 'D';
   if( average >= 70. && average < 80. ) return 'C';
   if( average >= 80. && average < 90. ) return 'B';
   if( average >= 90.                  ) return 'A';
 }

5.6 void Functions

Consider, we want to make a function just to output a message on the screen. We do not need it to return any value. In this case, we should use the void type specifier for the function.

In C++, void

  • is a special specifier indicating no type
  • is a signal to the compiler that no value will be returned
A simple example usage is given in Program 5.4 that outputs a message to the screen.

05prg04.cpp: A void function
  1:
  2:
  3:
  4:
  5:
  6:
  7:
  8:
  9:
 10:
 11:
 12:
 13:
 14:

// A simple void function
#include <iostream>
#include <string>
using namespace std;

void showMessage (string mess) {
   cout << mess << endl;
}

int main ()
{
  showMessage("This is a message.");
  return 0;
}
 
This is a message.

Although a void function returns no value, it can be used for a calculation. An example is illustrated in Program 5.5; the function printParts(x), outputs the real and integer parts of a float number x.

05prg05.cpp: Another void function
  1:
  2:
  3:
  4:
  5:
  6:
  7:
  8:
  9:
 10:
 11:
 12:
 13:
 14:
 15:
 16:
 17:
 18:
 19:
 20:
 21:

// Another void function
#include <iostream>
using namespace std;

void printParts (float x) {
   int i = int(x);
   float r = x - int(x);

   cout << "The number : " << x << endl;
   cout << "int part   : " << i << endl;
   cout << "real part  : " << r << endl;
}

int main ()
{
  float a = 13.72;

  printParts(a);

  return 0;
}
 
The number : 13.72
int part   : 13
real part  : 0.72

The void keyword can also be used in the function's parameter list to explicitly specify that we do not reqiure the function to take parameters. Imagine a function, printHello(), having no parameter and no type. 
  void printHello() {
    cout << "Hello" << endl;
  }
This is equivalent to: 
  void printHello(void) {
    cout << "Hello" << endl;
  }
In some documents you may see this usage for the main() function as well: 
  int main(void)
  {
     ...
  }

5.7 Many Functions

In a program sometimes it is necessary to use more than one function. This is actually based upon the concept of the procedural or structured programing.

Here a relatively advanced example is given. Consider we want to output the binomial coefficients defined by

These are actually the elements of a Pascal Triangle having the following form: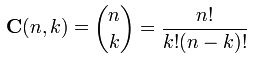 
   n = 1              1
   n = 2          1   2   1
   n = 3        1   3   3   1
   n = 4      1   4   6   4   1
   n = 5    1   5   10  10  5   1
   .        .
   .        .
   .        .
Here, we can define two functions: one for factorial of n, fact(n), and the other for the binomial coefficient C(n, k). Program 5.6 performs this task for n = 1, 2, 3, 4, 5 and 6 in a loop.

05prg06.cpp: Binomial coefficients
  1:
  2:
  3:
  4:
  5:
  6:
  7:
  8:
  9:
 10:
 11:
 12:
 13:
 14:
 15:
 16:
 17:
 18:
 19:
 20:
 21:
 22:
 23:
 24:
 25:
 26:
 27:
 28:
 29:
 30:
 31:
 32:
 33:
 34:
 35:
 36:

// Binomial coefficients
#include <iostream>
using namespace std;

// Function prototypes
int fact(int);
int C(int, int);

int main ()
{
  int n, k;

  for (n=0; n<=6; n++) {
     for (k=0; k<=n; k++) {
        cout << C(n, k) << '\t';
     }
     cout << endl;
  }

  return 0;
}

// Returns binomial coefficients
int C(int n, int k) {
   return ( fact(n)/(fact(k)*fact(n-k)) );
}

// Returns factorial of n (i.e. n!)
int fact(int n) {
  int i, f = 1;

  for(i=1; i<=n; ++i)
     f *= i;

  return f;
}
 
1
1   1
1   2   1
1   3   3    1
1   4   6    4    1
1   5   10   10   5    1
1   6   15   20   15   6   1

5.8 Examples

05prg07.cpp: Conversion of degrees to radians
  1:
  2:
  3:
  4:
  5:
  6:
  7:
  8:
  9:
 10:
 11:
 12:
 13:
 14:
 15:
 16:
 17:
 18:
 19:

// Convert an angle in degrees to radians.
#include <iostream>
using namespace std;

// prototypes
double rad(double);

int main () {
  double degrees, radians;
  cout << "Input the angle in degrees: ";
  cin >> degrees;
  radians = rad(degrees);
  cout << degrees << " Degrees = " << radians << " Radians." << endl;
}

double rad(double x) {
  const double pi = 3.14159265358979323846;
  return x*pi/180;
}
 
Input the angle in degrees: 45
45 Degrees = 0.785398 Radians.

05prg08.cpp: Table of sines and cosines
  1:
  2:
  3:
  4:
  5:
  6:
  7:
  8:
  9:
 10:
 11:
 12:
 13:
 14:
 15:
 16:
 17:
 18:
 19:
 20:
 21:
 22:
 23:
 24:
 25:
 26:
 27:
 28:
 29:

// Table of sines and cosines.
/*
 !------------------------------------------
 ! This program outputs a table of Sine and
 ! Cosines for the angles 0 to 90  in steps
 ! of 5 degrees.
 ! Modular programming is exaggerated. 
 !------------------------------------------
*/
#include <cmath>
#include <iostream>
using namespace std;

void lineout(int d);
double rad(double);

int main () {
  for (int deg=0; deg<=90; deg += 5) lineout(deg);
}

void lineout(int d) {
    cout.precision(5);
    cout << d << " " << sin(rad(d)) << " " << cos(rad(d)) << endl;
}

double rad(double x) {
  const double pi = 3.14159265358979323846;
  return x*pi/180;
}
 
0 0 1
5 0.087156 0.99619
10 0.17365 0.98481
15 0.25882 0.96593
20 0.34202 0.93969
25 0.42262 0.90631
30 0.5 0.86603
35 0.57358 0.81915
40 0.64279 0.76604
45 0.70711 0.70711
50 0.76604 0.64279
55 0.81915 0.57358
60 0.86603 0.5
65 0.90631 0.42262
70 0.93969 0.34202
75 0.96593 0.25882
80 0.98481 0.17365
85 0.99619 0.087156
90 1 6.123e-17

See topic 8 to learn how to neatly format this output.

05prg09.cpp: An n-cube tower
  1:
  2:
  3:
  4:
  5:
  6:
  7:
  8:
  9:
 10:
 11:
 12:
 13:
 14:
 15:
 16:
 17:
 18:
 19:
 20:
 21:
 22:

// A tower is built by stacking n cubes each of
// side length d. The surface area (excluding the
// base) is calculated using a function.
#include <iostream>
using namespace std;

double nCubeArea(int, double); // prototype

int main() {
  int n;
  double d;
  cout << "Input the number of cubes: ";
  cin >> n;
  cout << "Input the length of a side: ";
  cin >> d;
  cout << "The surface area of the tower is "
       << nCubeArea(n,d) << endl;
}

double nCubeArea(int k, double s) {
  return (4*k+1)*s*s;
}
 
Input the number of cubes: 8
Input the length of a side: 2.5
The surface area of the tower is 206.25

5.9 Exercises

  1. What are the differences between the function prototype and the function definition?
  2. If a function doesn't return a value, how do you declare the function?
  3. If you don't declare a return value, what type of return value is assumed?

  4. What is wrong with the function in the following code? 
    #include <iostream>
using namespace std;

void myFunc(unsigned short int x);

int main(void)
{
  unsigned short int a = 10, b;

  y = myFunc(int);
  cout << "a: " << x << " b: " << b << endl;

  return 0;
}

void myFunc(unsigned short int x){
  return (4*x);
}

  5. What is the output of the following program? 
    #include <iostream>
#include <cmath>
using namespace std;

int fun(int a) {
  int p = int(sqrt(a));
  int q = (a+10)%p;
  return (a + p + q);
}

int main()
{

  for(int i = 1; i <= 9; ++i) {
     int j = fun(i);
     cout << i << '\t' << j << endl;
  }

  return 0;
}

  6. Write a function named double perimeter(double r) which returns the circumference of a circle of radius r.

  7. Write a function that takes two integer arguments and returns the result of dividing the first by the second. The program should not attempt the division if the second number is zero, in this case it should return -1.

  8. Write a function named bool isEven(int x) that returns true if x is an even number or false otherwise.
    Hint: Use modulo operator (%). For example y = 1 for the operation y = x % 2 if x is an odd number.

  9. Write a boolean type function called bool isPrime(unsigned n) that returns true if n is a prime number or returns false otherwise.
    Hint: you can use the algorithm defined at: Sieve of Eratosthenes.

  10. In mathematics the Stirling's approximation (or Stirling's formula) is an approximation for large factorials. The formula is written as:
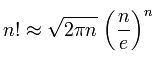
    Write a function named sfact(n) to calculate n! according to Stirling approximation. Note that return value of the function must be float or double since the formula generates real values.

  11. Write a main program that uses the functions fact(n) (defined in section 5.7) and sfact(n) (defined in the previous exercise), to compare the factorial of n = 0, 1, 2, ..., 10 by outputting the values of these functions. The output of the program should look something like this: 
     n       fact(n)   sfact(n)
===      =======   ========
  0      1         0
  1      1         0.922137
  2      2         1.919
  3      6         5.83621
  4      24        23.5062
  5      120       118.019
  6      720       710.078
  7      5040      4980.4
  8      40320     39902.4
  9      362880    359537
 10      3628800   3598700
[index][<][1][2][3][4][5][6][7][8][9][>]
please send us you comments/questions/corrections